Przykładowy schemat
Więc dla rozrywki znajdź analizę następującego obwodu:
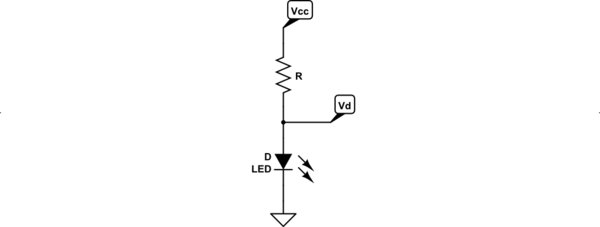
symuluj ten obwód - schemat utworzony przy użyciu CircuitLab
(Większość materiału, który tu przedstawiam, można łatwo znaleźć na tej stronie Wikipedii: modelowanie diod. Przyjmę jednak inne podejście do ich rozwiązania zamkniętego.)
Równanie diody Shockley
Zakładając działanie w temperaturze kalibracji, jedynym odpowiednim równaniem dla diody LED jest równanie diody Shockley:
$$ I_ \ text {D} = I_ \ text {SAT} \ left (e ^ {\ frac {V_ \ text {D}} {\ eta \, V_T }} - 1 \ right) $$
To równanie można łatwo przerobić, aby znaleźć \ $ V_ \ text {D} \ $ :
$$ V_ \ text {D} = \ eta \, V_T \, \ nazwa operatora {ln} \ left (\ frac {I_ \ text {D}} {I_ \ tekst {SAT}} + 1 \ right) $$
Mamy więc dwa różne spojrzenia na diodę / diodę LED.
W przypadku małosygnałowego BJT podłączonego do diody, zwykle jest tak, że współczynnik emisji (znany również jako współczynnik nieidealności ) wynosi \ $ \ eta = 1 \ $ . Ale w przypadku wielu dyskretnych diod, takich jak 1N4148 lub 1N4007, \ $ \ eta>1 \ $ . (Nie będzie mniej niż 1.) Niektóre diody LED będą miały dość wysokie wartości (przekraczające 4. nierzadko).
Prąd nasycenia \ $ I_ \ text {SAT} \ $ jest najlepiej postrzegany jako ekstrapolowany \ $ y \ $ -osi przecięcie z osią. Mówię o tym tutaj, a także tutaj i tutaj.
\ $ V_T = \ frac {k \, T} {q} \ $ to statystyczne napięcie termiczne i jest podstawowym parametrem fizycznym o wielu ważnych zastosowaniach. W temperaturze pokojowej często przyjmuje się, że jest to \ $ \ około 26 \: \ text {mV} \ $ .
Zamknięte rozwiązanie matematyczne
Równanie KVL dla powyższego obwodu to:
$$ \ begin {align *}
V_ \ text {CC} - R \, I_ \ text {D} - V_ \ text {D} & = 0 \: \ text {V} \\\\
V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V}
\ end {align *} $$
Problem polega na rozwiązaniu problemu dla \ $ I_ \ text {D} \ $ . Możesz łatwo rozwiązać ten problem w sposób iteracyjny. Lub, jeśli masz kartkę papieru z wykreślonym równaniem diody, możesz użyć linijki, aby dodać „linię obciążenia” rezystora i znaleźć przybliżony punkt przecięcia. Ale dla zamkniętego rozwiązania matematycznego bez iteracji potrzebujesz funkcji logu produktu (znanej również jako funkcja LambertW):
$$ \ begin {align *}
V_ \ text {CC} - R \, I_ \ text {D} - \ eta \; V_T \, \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right )} & = 0 \: \ text {V} \\\\
\ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ ln {\ left (\ frac {I_ \ text {D}} {I_ \ text {SAT}} \ right)} \\\\
e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T} - \ frac {R \, I_ \ text {D}} {\ eta \; V_T}}} & = \ frac { I_ \ text {D}} {I_ \ text {SAT}} \\\\
1 & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T} - \ frac {V_ \ text {CC}} {\ eta \, V_T}}} \\\\
e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {I_ \ text {D}} {I_ \ text {SAT}} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\\
\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} & = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {R \, I_ \ text {D}} {\ eta \, V_T}}} \\\ \
& \ text {set} u = \ frac {R \, I_ \ text {D}} {\ eta \, V_T} \\\\ & \ Dlatego \\\\
u \, e ^ u& = \ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T }}} \\\\
u& = \ nazwa operatora {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\
\ frac {R \, I_ \ text {D}} {\ eta \, V_T} & = \ nazwa operatora {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right) \\\\
I_ \ text {D} & = \ frac {\ eta \, V_T} {R} \ cdot \ nazwa operatora {LambertW} \ left (\ frac {R \, I_ \ text {SAT}} {\ eta \, V_T} \ cdot e ^ {^ {\ frac {V_ \ text {CC}} {\ eta \, V_T}}} \ right)
\ end {align *} $$
(Więcej informacji na temat funkcji dziennika produktu, znanej również jako LambertW, można znaleźć na stronie Wolfram's LambertW.)
Załóżmy teraz, że \ $ V_ \ text {CC} = 9 \: \ text {V} \ $ i \ $ R = 220 \: \ Omega \ $ . W przypadku diody LED użyjmy parametrów pobranych z diody LED Luminus PT-121-B: \ $ \ eta = 8.37 \ $ i \ $ I_ \ text {SAT} = 435,2 \: \ text {nA} \ $ . (Załóżmy oczywiście, że \ $ V_T \ około 26 \: \ text {mV} \ $ ). Wtedy znajdziemy \ $ I_ \ text {D} \ około 29,9 \: \ text {mA} \ $ i \ $ V_ \ text {D} \ około 2,42 \: \ tekst {V} \ $ . Jest to bardzo zbliżone do symulacji Spice dla urządzenia i okoliczności.
Lub załóżmy, że użyjemy parametrów dla 1N4148, \ $ \ eta = 1.752 \ $ i \ $ I_ \ text {SAT} = 2.53 \: \ text {nA} \ $ i użyj \ $ V_ \ text {CC} = 5 \: \ text {V} \ $ i \ $ R = 1 \: \ text {k} \ Omega \ $ . Następnie dla tej wspólnej diody znaleźlibyśmy \ $ I_ \ text {D} \ około 4,34 \: \ text {mA} \ $ i \ $ V_ \ text {D} \ około 654 \: \ text {mV} \ $ .
Jak widać, działa to dla wszystkich typów diod. (Głównym ograniczeniem jest fakt, że \ $ I_ \ text {SAT} \ $ różni się znacznie w zależności od temperatury - omówione pod koniec dyskusji na temat ' uproszczone modele diod ”, w których omówiono bardziej szczegółowo jej odchylenia wynikające z jednego z najważniejszych wyników mechaniki statystycznej, czynnika Boltzmanna).
Podsumowanie
Zamknięte rozwiązania podstawowych pytań dotyczących diod nigdy nie są podstawowe. Jednak w większości przypadków wystarczy przyjąć kilka upraszczających założeń i być „wystarczająco blisko do wszystkich celów i zamiarów”. (Aby przeczytać o niektórych z nich, zobacz „uproszczone modele diod”, o których wspomniano już chwilę temu.) Tak naprawdę prawdopodobnie nigdy nie będziesz musiał wykonywać powyższej pracy. Po prostu miło jest wiedzieć, o co chodzi, gdybyś się nad tym zastanawiał. (Przede wszystkim, więc zrozumiesz, dlaczego zamiast tego używasz tych upraszczających założeń).
Zwróć również uwagę, że zamknięte rozwiązanie jest rozwiązaniem na dużą skalę i rozwiązuje to pytanie w bardzo, bardzo szerokim zakresie okoliczności.
Zastanawiałeś się, co się stanie, gdy przyłożone napięcie jest równe napięciu diody. Ale w rzeczywistości napięcie diody dostosowuje się do okoliczności. To nie jest naprawione. Jeśli więc spróbujesz przyłożyć do obwodu tak zwane „napięcie diody”, dioda zamiast tego dostosuje swoje napięcie jeszcze niżej, tak aby spadek napięcia na rezystorze był „wystarczający”, aby zapewnić prąd „wystarczający” do uzyskać potrzebne napięcie diody, aby wyrównać różnicę. Oto prawdziwa odpowiedź. Powyższe rozwiązanie matematyczne jest po prostu skomplikowanym sposobem powiedzenia tego samego, ale ilościowo zamiast „machania ręką”.
Wszystkie powyższe mają zastosowanie dokładnie tak samo, jak w przypadku jakiejkolwiek diody spolaryzowanej do przodu. Nawet te o znacznej (w aplikacji) rezystancji ołowiu (która jest następnie dodawana do rezystancji szeregowej w celu analizy).