Jest taki ładny, mały (i niekompletny) zbiór zasad dotyczących obwodów cyfrowych, a dokładniej małych kulek:
- Małe kulki mogą podróżować po przewodach (nie zawsze Sekcje T)
- małe kulki mogą przemieszczać się przez bramki logiczne
- małe kulki neutralizują się nawzajem, gdy się zderzają
Druga wymaga niewielkiej ekspansji. Jeśli masz małą kulkę na wyjściu bramki AND, co czyni ją bramką NAND, możesz wziąć kulkę, podwoić ją, włożyć nowe kulki do wejścia i obrócić AND w OR. Podobnie jest, jeśli zaczniesz od bramki OR (która z małą kulką jest bramką NOR). Ktoś nazwij tę zasadę Prawa De Morgana, jeśli kiedykolwiek będziesz musiał to wyjaśnić nauczycielowi.
Wróć do swojego obwodu: weź dwie małe kulki, przejdź przez bramki NAND (rozdzielając kulki). Teraz masz dwie bramki OR i cztery kule. Przypomnijmy, że kula reprezentuje bramkę NOT:
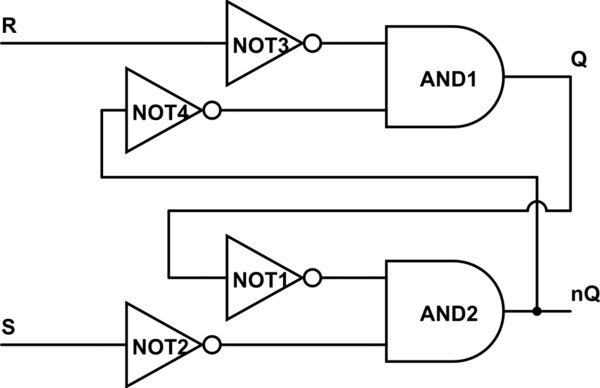
symuluj ten obwód - Schemat utworzony za pomocą CircuitLab
Teraz, jak widzisz, R i S są zanegowane, gdy tylko wejdą w obwód. Możemy zgodzić się i „uprościć” NOT3 z R i nazwać to wejście nR, podobnie jak S i NOT2.
Teraz wciśnijmy NOT4 aż do przecięcia T: co się tam dzieje? Cóż, możesz zanegować wynik AND i aby zachować niższą wartość nQ, powinieneś tam również umieścić nie.
Diagram jest wart tysiąca słów:
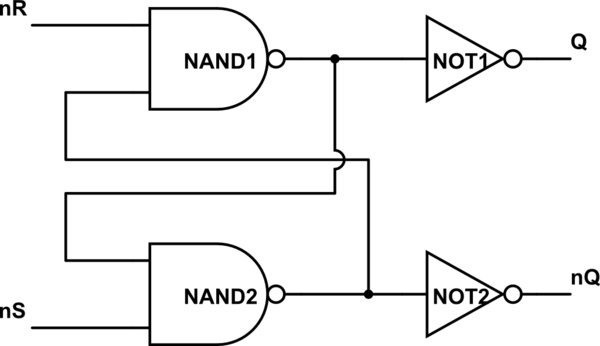
symuluj ten obwód
Teraz możesz uprościć Q i NOT1 i oznaczyć to, co generuje nQ oraz uprościć nQ i NOT2 oraz etykietę to wyjście P. Czy obwód wygląda teraz bardziej znajomo? Twój drugi obwód jest taki sam, tylko to, co nazywasz ustawianiem i resetowaniem zmian.
Prawdziwe pytanie brzmi: dlaczego zawracałem sobie głowę tą całą historią o „małych kulkach”? Mogłeś po prostu zapisać tabelę prawdy i „łatwo” zobaczyć, co się dzieje. Cóż, myślę, że przesuwanie małych kulek bardzo pomaga w rozwiązywaniu prostych problemów, a nawet tych nieco bardziej skomplikowanych. Poza tym jest to fajna .